Wczytanie zmiennych, ustalenie zmiennych zależnych i niezależnych:

# Importing the libraries
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd

# Importing the dataset
dataset = pd.read_csv('Position_Salaries.csv')
X = dataset.iloc[:, 1:2].values
y = dataset.iloc[:, 2].values

Uwaga: zmienna X pomimo, że zawiera jedną kolumnę, została zdefiniowana w taki sposób, żeby była reprezentowana jako macierz jednokolumnowa.

Ponieważ regresja wielomianowa jest nadal regresją liniową w pierwszym kroku należy przygotować macierz zmiennych niezależnych w taki sposób, aby reprezentowała wartości zgodne z funkcją wielomianową, która spodziewamy się, że dobrze odwzoruje nasze dane.

# Fitting Polynomial Regression to the dataset
from sklearn.preprocessing import PolynomialFeatures
poly_reg = PolynomialFeatures(degree = 2)
X_poly = poly_reg.fit_transform(X)

Takie wywołanie zwraca w wyniku macierz, która w pierwszej kolumnie zawiera stałą 1 (odzwierciedlenie wyrazu wolnego), w drugim wartość zmiennej wejściowego, a w trzeciej wartość zmiennej wejściowej podniesionej do kwadratu. Parametr degree oznacza stopień funkcji wielomianowej

Teraz nie pozostaje nic innego jak stworzyć model regresji liniowanej dla którego zmienną wejściową będzie nowa macierz z wartościami charakterystycznymi dla funkcji wielomianowej (w naszym przypadku kwadratowej)

lin_reg_2 = LinearRegression()
lin_reg_2.fit(X_poly, y)

Ponieważ mamy tylko jedną zmienną niezależną i jedną zależną, łatwo zwizualizować wynik działania modelu:

plt.scatter(X, y, color = 'red')
plt.plot(X, lin_reg_2.predict(poly_reg.fit_transform(X)), color = 'blue')
plt.title('Truth or Bluff (Polynomial Regression)')
plt.xlabel('Position level')
plt.ylabel('Salary')
plt.show()

Możemy ten model udoskonalić zmieniając stopień wielomianu. Przy stopniu 3, dostaniemy wykres:

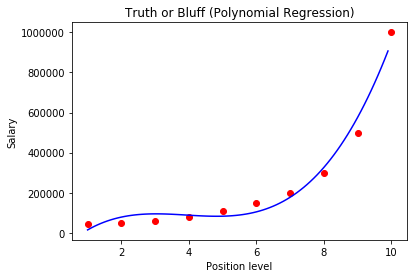
A przy stopniu równym 4 jest prawie idealnie:

Predykcja dla nowej wartości:

lin_reg_2.predict(poly_reg.fit_transform(6.5))